Understanding the Z Factor in Pipette Calibration
Pipettes are essential tools in laboratories, enabling researchers and scientists to measure and transfer precise volumes of liquid. Ensuring that pipettes deliver accurate volumes is critical to achieving reliable experimental results. Calibration is, therefore, an indispensable part of pipette maintenance. One of the often-discussed factors in pipette calibration is the Z factor, a variable that helps in making accurate volume measurements, especially when temperature fluctuations are present. This article explores the significance of the Z factor, how it is calculated, and its impact on pipette calibration.
What is the Z Factor?
The Z factor is a temperature-dependent coefficient used to convert the mass of water dispensed by a pipette into volume. Since pipettes are typically calibrated using water, and because water density varies with temperature, this factor is crucial in correcting for these density changes. Essentially, the Z factor accounts for the volume discrepancy that occurs due to the difference in water density at different temperatures, allowing for more accurate volume calibration regardless of environmental conditions.
Why is the Z Factor Important in Pipette Calibration?
Since pipettes measure liquids in terms of volume, any mass-based measurement during calibration requires conversion to volume. Water, the standard calibration fluid, has a density that varies with temperature, so without the Z factor, any calibration could be inaccurate if the ambient temperature changes. The Z factor corrects for this temperature variability by linking mass measurements to actual volume at specific temperatures.
For instance, at a standard reference temperature (usually 20°C), water has a density of approximately 0.9982 g/mL. However, at different temperatures, this density shifts, and so does the apparent volume of dispensed water if we only consider mass. The Z factor allows technicians to adjust for these shifts, ensuring the calibration remains precise regardless of minor temperature changes.
The Formula for the Z Factor
The Z factor is calculated using the formula:
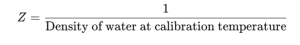
This formula means that as the temperature changes, the Z factor adjusts in relation to the density of water at that specific temperature. When applied during calibration, the Z factor converts the mass of dispensed water into an accurate volume measurement.
Example of Z Factor Values at Different Temperatures
| Temperature (°C) | Density of Water (g/mL) | Z Factor (mL/g) |
| 15 | 0.9991 | 1.0009 |
| 20 | 0.9982 | 1.0018 |
| 25 | 0.9970 | 1.0030 |
As seen from the table, the Z factor slightly increases as the temperature rises due to the decrease in water density.
Applying the Z Factor in Pipette Calibration
-
- Weighing the Dispensed Liquid: During calibration, the technician dispenses a set amount of water from the pipette and weighs it. The mass (in grams) of the water is recorded.
-
- Determining the Calibration Temperature: The ambient temperature is noted, as it directly influences the density of water.
-
- Using the Z Factor: Based on the temperature, the appropriate Z factor is selected. By multiplying the measured mass by the Z factor, the technician calculates the actual dispensed volume in milliliters.
![]()
-
- Comparison with Target Volume: The calculated volume is then compared with the target volume. If discrepancies exceed acceptable tolerance limits, adjustments to the pipette are made.
Practical Considerations for Using the Z Factor
-
- Temperature Control: Laboratories should ideally maintain a stable temperature during pipette calibration, minimizing the need for Z factor adjustments. If this is not feasible, recalibrations should be made frequently with the Z factor in mind.
-
- Regular Calibration: Pipettes should undergo routine calibration to account for potential drifts in accuracy and ensure that any Z factor adjustments are applied correctly.
-
- Calibration Standards and Protocols: ISO 8655-6, a widely recognized standard, provides guidelines on using the Z factor and other variables in pipette calibration, helping to standardize practices across labs.
Challenges and Limitations
While the Z factor effectively corrects for density changes in water, it does not account for all environmental variables. Humidity, barometric pressure, and pipette type can also affect accuracy. Additionally, while the Z factor helps improve precision, it assumes the technician uses highly accurate scales and follows proper procedures. Minor errors in handling, such as not properly accounting for evaporation or inconsistencies in dispensing techniques, can still lead to inaccuracies.
Conclusion
The Z factor is a vital correction tool in pipette calibration, accounting for temperature-induced density changes in water. By converting mass measurements into accurate volume measurements, the Z factor enables more precise calibration, enhancing experimental reliability. As labs strive for consistent results, understanding and applying the Z factor during pipette calibration helps maintain high standards and supports quality data production across scientific fields.
Z-Correction Factors for Distilled Water Based on Test Temperature and Air Pressure
| Temp (°C) | Air pressure (kPa) | ||||||
| 80 | 85 | 90 | 95 | 100 | 1013 | 105 | |
| 15,0 | 10017 | 10018 | 10019 | 1,0019 | 10020 | 10020 | 10020 |
| 15,5 | 10018 | 10019 | 10019 | 1,0020 | 10020 | 10020 | 10021 |
| 16,0 | 10019 | 10020 | 10020 | 1,0021 | 10021 | 10021 | 10022 |
| 16,5 | 10020 | 10020 | 10021 | 1,0021 | 10022 | 10022 | 10022 |
| 17,0 | 10021 | 10021 | 10022 | 1,0022 | 10023 | 10023 | 10023 |
| 17,5 | 10022 | 10022 | 10023 | 1,0023 | 10024 | 10024 | 10024 |
| 18,0 | 10022 | 10023 | 10023 | 1,0024 | 10025 | 10025 | 10025 |
| 18,5 | 10023 | 10024 | 10024 | 1,0025 | 10025 | 10026 | 10026 |
| 19,0 | 10024 | 10025 | 10025 | 1,0026 | 10026 | 10027 | 10027 |
| 19,5 | 10025 | 10026 | 10026 | 1,0027 | 10027 | 10028 | 10028 |
| 20,0 | 10026 | 10027 | 10027 | 1,0028 | 10028 | 10029 | 10029 |
| 20,5 | 10027 | 10028 | 10028 | 1,0029 | 10029 | 10030 | 10030 |
| 21,0 | 10028 | 10029 | 10029 | 1,0030 | 10031 | 10031 | 10031 |
| 21,5 | 10030 | 10030 | 10031 | 1,0031 | 10032 | 10032 | 10032 |
| 22,0 | 10031 | 10031 | 10032 | 1,0032 | 10033 | 10033 | 10033 |
| 22,5 | 10032 | 10032 | 10033 | 1,0033 | 10034 | 10034 | 10034 |
| 23,0 | 10033 | 10033 | 10034 | 1,0034 | 10035 | 10035 | 10036 |
| 23,5 | 10034 | 10035 | 10035 | 1,0036 | 10036 | 10036 | 10037 |
| 24,0 | 10035 | 10036 | 10036 | 1,0037 | 10037 | 10038 | 10038 |
| 24,5 | 10037 | 10037 | 10038 | 1,0038 | 10039 | 10039 | 10039 |
| 25,0 | 10038 | 10038 | 10039 | 1,0039 | 10040 | 10040 | 10040 |
| 25,5 | 10039 | 10040 | 10040 | 1,0041 | 10041 | 10041 | 10042 |
| 26,0 | 10040 | 10041 | 10041 | 1,0042 | 1.0042 | 10043 | 10043 |
| 26,5 | 10042 | 10042 | 10043 | 1,0043 | 10044 | 10044 | 10044 |
| 27,0 | 10043 | 10044 | 10044 | 1,0045 | 10045 | 10045 | 10046 |
| 27,5 | 10045 | 10045 | 10046 | 1,0046 | 10047 | 10047 | 10047 |
| 28,0 | 10046 | 10046 | 10047 | 1,0047 | 10048 | 10048 | 10048 |
| 28,5 | 10047 | 10048 | 10048 | 1,0049 | 10049 | 10050 | 10050 |
| 29,0 | 10049 | 10049 | 10050 | 1,0050 | 10051 | 10051 | 10051 |
| 29,5 | 10050 | 10051 | 10051 | 1,0052 | 10052 | 10052 | 10053 |
| 30,0 | 10052 | 10052 | 10053 | 1,0053 | 10054 | 10054 | 10054 |